Difference between revisions of "Centroid"
(Updated United Kingdom) Tags: Mobile edit Mobile web edit |
(Updated France) Tags: Mobile edit Mobile web edit |
||
| Line 58: | Line 58: | ||
| Finland || Helsinki || || 5 || [https://docs.google.com/spreadsheets/d/1OXHdXZDUJ9So5oSP67ZWzkDdSaQADQdZbDMnp7ekXcU/ link] | | Finland || Helsinki || || 5 || [https://docs.google.com/spreadsheets/d/1OXHdXZDUJ9So5oSP67ZWzkDdSaQADQdZbDMnp7ekXcU/ link] | ||
|- | |- | ||
| − | | France || Paris || || | + | | France || Paris || Lyon || 7 || [https://docs.google.com/spreadsheets/d/1-G7VVZDE7xH6yzhsVYpmTTnu3rtgvadMC7WX9yIJqPc link] |
|- | |- | ||
| Germany || Hannover || || 19 || [https://docs.google.com/spreadsheets/d/1HSNFq2sJiRxarSvY_mHtEOiSIq9fwFAyTh9lA4DfgF4 link] | | Germany || Hannover || || 19 || [https://docs.google.com/spreadsheets/d/1HSNFq2sJiRxarSvY_mHtEOiSIq9fwFAyTh9lA4DfgF4 link] | ||
Revision as of 10:15, 4 March 2021
The centroid of a country (or area) can de defined in multiple ways. On the earth surface it is more useful to speak of the geographical center. It is possible to find lists of these centers for area's on earth. (parent page)
One quickly realises that these centers are not (always) good enough. Either they are in a location far away from population centers, or they fall in between a set of islands, etc. So we need to come up with a better estimate.
Any better estimate must reflect what we intend to achieve in the first place. We are talking about transportation and its impact. So we talk about distances, mode of transportation, the amount transported and the impact of it all. Any centroid should take this into account.
If we know only the country a product is bought in, we can either assumes the worst or the best. The worst is the maximum impact and the best the minimum impact. The minimum impact will imply transportation from the most centered location in a country.
What is now the most centered location? The distances to all other locations should be small as possible. And the usage of these distances should be as small as possible. This will take into account the population sizes of all the locations.
This seems to be a Weber problem. This problem is not solvable exactly, but must be solved iteratively. The locations are then the towns and cities in a country. And the weights are defined by the population sizes of each towns. And the distances are defined by the distances by road.
In practice it will be quite difficult to solve this for all towns in an area. But can we do it for the largest towns? And how many towns should we incorporate?
Recipe
Using the above considerations we can setup a recipe:
- Largest cities - find the largest cities (by population size) for a country. Star with the 5 largest cities;
- Population - list the population size for each of the largest cities, and calculate the fraction of the total population of all largest cities;
- distances - calculate the distances between all the largest cities. We can use the directions of OpenStreetMap for this;
- weighted distance - calculate the weighted distances, i.e. the distance times the city fraction;
- weighted distance sum - add all the weighted fractions for a specific city (the centroid city);
- minimum weighted distance sum - find the weighted distance sum that is the lowest. The corresponding city is the centroid city;
- add cities - more cities can be added to see whether the found centroid city is correct. For this recommence on step 1;
Spreadsheet
The recipe described above has been implemented in a Google spreadsheet. For each country (territory) a separate spreadsheet needs to be created (just copy an existing) one. Each spreadsheet has multiple worksheets.
- population worksheet: this worksheet lists the largest cities and their population (as columns), ordered by the population. The fraction is calculated from the data;
- distance worksheet: this worksheet contains the distances between the cities noted on the population spreadsheet. The distances are taken from OpenStreetMap. Only the fields above the diagonal need to be filled. The fields below the diagonal are filled subsequently;
- weighted sum: this worksheet is calculated based on the two worksheets mentioned above. The row at the bottom (the one without a city) is the sum of a column. The column with the smallest sum is the city we are looking for. To determine the quality of this city, the entries weighted dethroning distance, dethroning distance and real distance need to be changed. The weighted dethroning distance should have the weighted sum of the runnerup city minus the weighted sum of the centroid city. The dethroning distance is the weighted dethroning distance divided by the population fraction of the latest city that has been added. And the real distance is a reference to the real distance between the centroid and runnerup city. The larger the difference betzeen dethroning distance and real distance, the better the quality;
- growth worksheet: this worksheet allows to see how the weighted sums grow with each added city. Especially to see what happens between the centroid and runnerup city;
Result
This recipe has been applied on the following countries:
| Country | Centroid city | Runnerup city | quality | spreadsheet |
|---|---|---|---|---|
| Albania | Tirana | Kamëz | 13 | link |
| Algeria | Algers | link | ||
| Austria | Vienna | 184 | link | |
| Belgium | Brussels | 0.7 | link | |
| Bosnia and Herzegovina | Zenica | 0.6 | link | |
| Croatia | Zagreb | link | ||
| Czech Republic | Prague | 9 | link | |
| Denmark | Copenhagen | 16 | link | |
| Estonia | Tallinn | Maardu | 12 | link |
| Finland | Helsinki | 5 | link | |
| France | Paris | Lyon | 7 | link |
| Germany | Hannover | 19 | link | |
| Greece | Athens | link | ||
| Hungary | Budapest | link | ||
| Iceland | Reykjavik | Kópavogur | 10 | link |
| Ireland | Dublin | 56 | link | |
| Italy | Rome | Florence | 0.6 | link |
| Latvia | Riga | 25 | link | |
| Lithuania | Kaunas | link | ||
| Montenegro | Bijelo Polje | 15 | link | |
| Morocco | Temara | link | ||
| Netherlands | Utrecht | Amsterdam | 4 | link |
| Norway | Skien | Oslo | 0.7 | link |
| Poland | Łódź | Warschau | 24 | link |
| Portugal | Lisboa | 0.5 | link | |
| Romania | Bucharest | Ploiești | 4 | link |
| Slovakia | Banská Bystrica | link | ||
| Slovenia | Ljubljana | Domžale | 74 | link |
| Spain | Madrid | Barcelona | 1.1 | link |
| Sweden | Nörrköping | Stockholm | 3 | link |
| Switzerland | Olten | 36 | link | |
| Tunisia | Tunis | link | ||
| United Kingdom | Coventry | Leicester | 12 | link |
| European Union | Munich | Prague | 0.3 | link |
| Bouches du Rhône | Marseille | Les Pennes Mirabeau | 30 | link |
This approach of finding a centroid seems to give good results. As more cities are added the centroid does not change for most countries.
For small countries, it is clear that the major city should be used as Centroid. Think of Andorra, Liechtenstein, Monaco and San Marino.
Explanation:
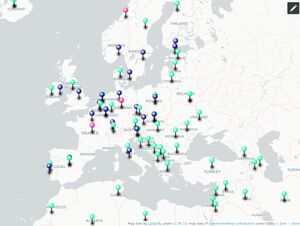
- blue pins - population centroids
- green pins - geographic centroids
- red pins - wikipedia centroids (barycenters)
- dots - cities in second place
Country Remarks
The city population centroids have been found a step by step process. This allows to see how the centroid changes after a city has been added. In general the largest city dominates the position of the centroid. And if that city is also close to the geographic centroid, it will be the centroid in the end (Belgium, Spain). If a large city is surrounded by other cities, then one of those can become the centroid (Norway, Switzerland). The layout of motorways can influence the selection between two cities (France).
In general we see that the largest city is also the centroid city, when it is really much larger than the other cities.
Some exceptions to this:
- Belgium - the runnerup is Mechelen, so if more cities are added, the centroid might move towards that city along the motorway;
- France - the centroid lies along the motorway between Paris and Lyon. There are no cities that are large enough in the top 20 to push the centroid away from Paris towards Lyon. Adding Dijon did not help. Probably due to a lack of motorways to the west from Dijon;
- Germany - the country is dominated by Berlin. Only thanks to the existence of a large town to the west, the centroid could be moved there (Hannover);
- Italy - the centroid is dominated by Rome, but might move upwards towards Florence, when more cities in the populous north are added;
- Lithuania - the medium sized cities Kaunas;
- Morocco - the centroid lies along the coast between the large cities Casablanca and Rabat;
- Netherlands - as expected in Utrecht. This is in the center of the country and also a center of motorways;
- Norway - the centroid is in Skien, but could have been in Oslo, or in between these two cities. The centroid is much lower than the actual geographic centroid;
- Poland - largest cities are spread out, so Łódź lies in between;
- Slovakia - there are several small towns fighting to centroid. Banská Bystrica was able to fend them off;
- Spain - Madrid is very well placed centrally in the country. Madrid and Barcelona are the greatest influencers on the centroid. The cities on the Canaries have been removed, but the Baleares have been kept.
- Sweden - the country is dominated by the Stockholm and surrounded cities. Due to the cities close to Denmark, the centroid is moved to the south.
- Switzerland - Olten is one of the smaller towns in the valleys around Zurich, which dominates the centroid. Note that for transport a route through Italy is sometimes more advantageous.
- United Kingdom - Although the UK is dominated by London, there are a lot of large cities to the north. This is the reason Coventry is the centroid.
Quality
How good are these centroids? What happens when more cities are added? How good is good enough?
Required accuracy
The eco-score label reduces every score (0-100) to just 5 levels . Each level represents a score range of 20. So the maximum bonus of 15 (which is part of the score) might change the eco-score level. Thus the accuracy required should be of the order of a bonus point.
The transportation score is multiplied by 0.15 to get the bonus points. An accuray of 1 bonus point thus implies a accuracy of 7 transportation score.
The normalisation of 2000 km for 100 transportation score points, implies 20km per transportation score points. And a a transportation score of 7 is thus 140km.
So if we get an accuracy of 100 km the centroid cities are good enough.
Actual accuracy
Can the accuracy of the centroid city be determined from the actual calculations, or their development? Every time another city is added, the centroid might change. But how likely is it that this happens. That depends on the size and relative population of the added city. And it depends on weighted distance to the runnerup centroid city. If the weighted distance is very large, adding other cities will not budge the winner city.
So calculate the difference in weighted distance between the winner centroid city and the runner-up centroid city. Divide this by the fractional size of the latest city added. This will result in a dethroning distance. This dethroning distance is the distance required to dethrone the winner city. (In practice this required distance will be much larger)
If this dethroning distance is larger than the size of the country, the winner centroid is ok. If the dethroning distance is smaller, then we have to take a closer look. As the dethroning distance will be much larger, we should only look at cases where the dethroning distance is smaller than the actual distance.
In the calculated centroids, this implies:
- France (between Paris and Lyon)
- Norway (between Oslo and Skien)
- Portugal (between Lisboa and Odivelas)
- United Kingdom (between Leicester and London)
Should we bother from transportation score point of view? Not for Norway and Portugal. For France and United Kingdom more cities should be added.
- United Kingdom the centroid moved to Coventry after adding the city;
- France stays difficult, adding another 5 cities caused a switch from Paris to Lyon. Adding cities in between (Auxerre, Chalons) did not help.
Observations
Can this approach also be used to get an indication of country size?