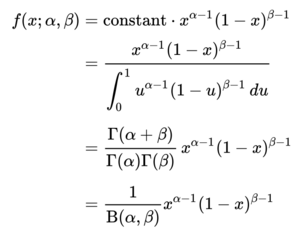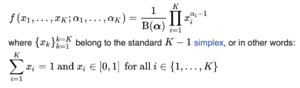Nutritional values probability theory
When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This might for instance help to detect subgroups and unusual products. Plotting the individual values of products in the group is already very useful, but one likes to do more.
The usual tools for determining an average and distribution is to assume that the probability distribution of the nutritional values follows a normal gaussian distribution. Using a gaussian distribution assumes that the values can get any value: from minus infinity to plus infinity. For nutritional values this is not the case. Nutritional values are fractions that go from 0 to an upper limit. For Energy this upper limit is 3700 kJ and for the nutrients this is 1. The Energy limit is reached if 100% of the nutrients consist of oil for instance.
That the normal distribution cannot be used is very well demonstrated by the Violin plots. Underlying the graph is the assumption of a normal distribution. This in turn leads to a plot that can go below zero.
If a normal distribution cannot be used, what should be used then? Some other probability distribution should be used.
Note: this page limits itself to statistical considerations for nutritional values. There is much material available on Internet, which describes things much better. The page page is more about what should and can be applied to nutritional values.
Probability distribution
There exist many probability distributions, so which one is applicable to nutritional values. What we are looking for lies in the category of continuous distributions, which means that the nutritional values are Real numbers. And the distribution should be on a bounded interval. The most general of these distributions is the Beta distribution.
Beta distribution
The formula for the beta distribution is give in the figure below.
In the formula the values x are between 0 and 1. The α and β determine the shape of the function. The Γ(z) is the Gamma function. The parameters α and β are positive integers (not 0).
Probably α and β will roughly equal for most nutritional values. If the nutritional value is close to 0, α=1 and β is large; if the nutritional value is close to 1, α is large and β=1.
The mean is define by α/(α+β) and the variance by αβ/[(αβ)2(α+β+1)].
Applicability
Is this distribution applicable to the nutritional values of the groups of products? And when is it not? And how would be able to detect that? If there are within a group two different subgroups that have clearly different nutritional values, then it is obvious this distribution can not be applied. And the subgroups should be analysed separately.
Scaling
The Beta distribution assumes that the x-values are between 0 and 1. The nutritional values published on products are either in grams per 100 gram or in grams per serving. The Energy values are in KJ (or kcal) per 100 grams (or per serving). All these numbers need to be scaled, so that they are between 0 and 1.
We have now two possibilities:
- the nutrients of a product are analysed by weight, i.e. what weight fraction of a product is due a certain nutrient;
- the nutrients of a product are analysed by energy, i.e. what energy fraction of a product is due to a certain nutrient
The energy must be scaled differently and the maximum allowed value of 3700 kJ should be used to scale the values.
Is this scaling sufficient? The minimum value is always 0. But the maximum value is not always 1, but that depends on other the existence of other nutrients and components. If we use another maximum value the formula above should be adapted.
Multivariate considerations
The beta function described above assumes that the nutritional values are uniformly distributed between 0 and 1. This unfortunately is not always the case. If a product consists of one nutrient this is correct. But if there are more than one nutrient, only the sum of all nutrients is between 0 and 1. A single nutrient has than a maximum that is smaller than 1. But we do not know that maximum beforehand.
The published macronutrients do not represent 100% of the weight of a product. For instance water represents a large fraction by weight of a product, but its value is unknown. Even not all macronutrients are always available (fiber).
Dirichlet distribution
Thus there is an interdependence between the maxima of each nutrient, which is set by the total. A Dirichlet distribution would be more applicable.
This Beta distribution is a special case of the Dirichlet distribution. The Dirichlet distribution is described by 5 axes (fat, carbohydrates, fiber, protein, salt). Each of the axes has its own parameter αi.
The sum of all the α's gives the αtotal. This is used the mean and variance for each axis, i.e. Meani= αi/αtotal. And the variance: αi(αtotal-αi)/(α02(αtotal-1)).
If we look only at a single nutrient, the corresponding Beta-distribution is defined by: Beta(αi, αtot-αi), thus the β of the Beta distribution is αtot-αi
Energy
The Dirichlet distribution can only be used for the nutrients, as the sum of the nutrients is 1 (100% of the product weight). Thus we cannot include the Energy in the formula. Something that is more generalised is required.
The first thing to look at is the Generalized Dirichlet which doubles the parameters for each axis. But is not clear if this would be helpful. No useful examples can be found. A critique of the Dirichlet distribution is the restricted covariance matrix.
Sub-nutrients
For some macronutrients, there are also sub-nutrients. For instance for fat, saturated fat. And for carbohydrates the sugars. Could the play a role in a probability distribution? A keyword might be Nested Dirichlet distributions.
Estimates
The nutritional values for a group of products can be used to estimate the values of the beta function. From wikipedia:
It is also possible to estimate the maximum of the distribution, which we might need if we want to do things correct. The wikipedia page gives an extensive explanation. This analysis needs to be redone as we need to constrain any value to the lower limit of zero.
The above functions do not work in practice as the observed distributions have a variance that is too large. A maximum likelihood method should be used instead. An explication can be found here.
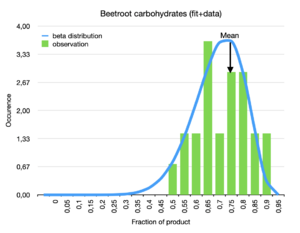
The figure shows a fit of the carbohydrates values of Canned beetroot. The line is the fit to the data with a Beta distribution function. This function has an alpha of 11.6 and a beta of 4.1, implying a mean of 0.75, i.e. 75% of the nutrients in Canned beetroot are due to carbodydrates.
Violin plots
For violin plots an adapted Kernel Density Function must be used, which uses the beta probability distribution. The advice is to cut the kernel functions at the bounds 0 and 1.
Upper limit values
Note that any value in a nutritional table that is indicated by an upper limit (i.e. <) should be replace by zero (0). However this might bias the actual distribution to 0. And if we use the limits as actual values we might bias the actual distribution to a too high level.