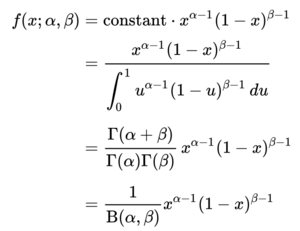Nutritional values probability theory
When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This might for instance help to detect subgroups and unusual products. Plotting the individual values of products in the group is already very useful, but one likes to do more.
The usual tools for determining an average and distribution is to assume that the probability distribution of the nutritional values follows a normal gaussian distribution. Using a gaussian distribution assumes that the values can get any value: from minus infinity to plus infinity. For nutritional values this is not the case. Nutritional values are fractions that go from 0 to an upper limit. For Energy this upper limit is 3700 kJ and for the nutrients this is 1. The Energy limit is reached if 100% of the nutrients consist of oil for instance.
That the normal distribution cannot be used is very well demonstrated by the Violin plots. Underlying the graph is the assumption of a normal distribution. This in turn leads to a plot that can go below zero.
If a normal distribution cannot be used, what should be used then? Some other probability distribution should be used.
Probability distribution
There exist many probability distributions, so which one is applicable to nutritional values. What we are looking for lies in the category of continuous distributions, which means that the nutritional values are Real numbers. And the distribution should be on a bounded interval. The most general of these distributions is the Beta distribution.
Beta distribution
The formula for the beta distribution is give in the figure below.
In the formula the values x are between 0 and 1. The α and β determine the shape of the function. The Γ(z) is the Gamma function, i.e (z-1)! The parameters α and β are positive integers (not 0).
Probably α and β will roughly equal for most nutritional values. If the nutritional value is close to 0, α=1 and β is large; if the nutritional value is close to 1, α is large and β=1.
The mean is define by α/(α+β) and the variance by αβ/[(αβ)2(α+β+1)].
Scaling
The Beta distribution assumes that the x is between 0 and 1. For the Energy this is not the case as the maximum allowed value is 3700 kJ. One has to scale the x values, so that they lie between 0 and 1.
Multivariate considerations
The beta function described above assumes that the nutritional values are normally distributed between 0 and 1. This unfortunately is not always the case. I a product consists of one nutrient this is correct. But if there are more than one nutrient, only the sum of all nutrients is between 0 and 1. A single nutrient has than a maximum that is smaller than 1. But we do not know the maximum beforehand.
Should the maximum of the published macronutrients be 100? Do the published macronutrients (fat, carbohydrates, fiber, proteins, salt) add up to 100%, or are the also other macronutrients that should have been included? If no fiber values is published the sum will certainly be less than 100%.
Thus there is an interdependence between the maxima of each nutrient, which is set by the total. Some kind of multivariate beta distribution would be more in place.
Adding energy
How could a probability distribution include the energy component? The energy is expressed as a function between the nutrients, thus adding an additional constraint.
Sub-nutrients
For some macronutrients, there are also sub-nutrients. For instance for fat, saturated fat. And for carbohydrates the sugars. Could the play a role in a probability distribution?
Finding the correct probability distribution sounds like a student project.
Estimates
The nutritional values for a group of products can be used to estimate the values of the beta function. From wikipedia:
It is also possible to estimate the maximum of the distribution, which we might need if we want to do things correct. The wikipedia page gives an extensive explanation. This analysis needs to be redone as we need to constrain any value to the lower limit of zero.
The above functions do not work in practice as the observed distributions have a variance that is too large.
Violin plots
For violin plots an adapted Kernel Density Function must be used, which uses the beta probability distribution. The advice is to cut the kernel functions at the bounds 0 and 1.
Upper limit values
Note that any value in a nutritional table that is indicated by an upper limit (i.e. <) should be replace by zero (0).