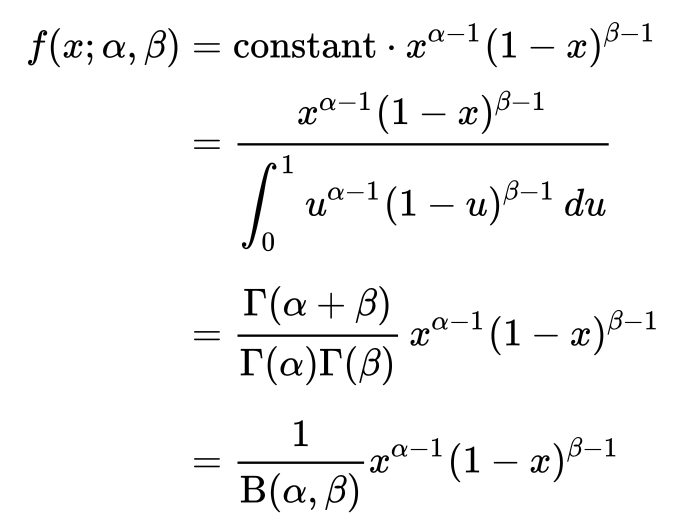Difference between revisions of "Nutritional values probability theory"
(Created page with "When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This...") |
|||
| Line 1: | Line 1: | ||
When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This might for instance help to detect subgroups and unusual products. Plotting the individual values of products in the group is already very useful, but one likes to do more. | When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This might for instance help to detect subgroups and unusual products. Plotting the individual values of products in the group is already very useful, but one likes to do more. | ||
| − | The usual tools for determining an average and distribution is to assume that the probability distribution of the nutritional values follows a normal gaussian distribution. Using a gaussian distribution assumes that the values can get any value: from minus infinity to plus infinity. For nutritional values this is not the case. Nutritional values are fractions that go from 0 to an upper limit. For Energy this upper limit is 3700 kJ and for the nutrients this is 1. The Energy limit is reached if 100% of the nutrients consist of oil for instance. | + | The usual tools for determining an average and distribution is to assume that the probability distribution of the nutritional values follows a [https://en.wikipedia.org/wiki/Normal_distribution normal gaussian distribution]. Using a gaussian distribution assumes that the values can get any value: from minus infinity to plus infinity. For nutritional values this is not the case. Nutritional values are fractions that go from 0 to an upper limit. For Energy this upper limit is 3700 kJ and for the nutrients this is 1. The Energy limit is reached if 100% of the nutrients consist of oil for instance. |
That the normal distribution cannot be used is very well demonstrated by the [[Visualisation/Violinplot|Violin plots]]. Underlying the graph is the assumption of a normal distribution. This in turn leads to a plot that can go below zero. | That the normal distribution cannot be used is very well demonstrated by the [[Visualisation/Violinplot|Violin plots]]. Underlying the graph is the assumption of a normal distribution. This in turn leads to a plot that can go below zero. | ||
| − | If a normal distribution cannot be used, what should be used then? | + | If a normal distribution cannot be used, what should be used then? Some other [https://en.wikipedia.org/wiki/Probability_distribution probability distribution] should be used. |
| + | |||
| + | == Probability distribution == | ||
| + | There exist many [https://en.wikipedia.org/wiki/List_of_probability_distributions probability distributions], so which one is applicable to nutritional values. What we are looking for lies in the category of continuous distributions, which means that the nutritional values are Real numbers. And the distribution should be on a [https://en.wikipedia.org/wiki/List_of_probability_distributions#Supported_on_a_bounded_interval bounded interval]. The most general of these distributions is the [https://en.wikipedia.org/wiki/Beta_distribution Beta distribution]. | ||
| + | === Beta distribution === | ||
| + | The formula for the beta distribution is give in the figure below. | ||
| + | [[File:BetaProbabilityDistribution.png|100px|frame|center]] | ||
| + | In the formula the values x are between 0 and 1. The α and β determine the shape of the function. No idea what kind of values these α and β will have for nutritional values. | ||
Revision as of 07:30, 6 October 2024
When analysing the nutritional values of groups as products, such as categories, one likes to know what the expected value and spread around that values of that group is. This might for instance help to detect subgroups and unusual products. Plotting the individual values of products in the group is already very useful, but one likes to do more.
The usual tools for determining an average and distribution is to assume that the probability distribution of the nutritional values follows a normal gaussian distribution. Using a gaussian distribution assumes that the values can get any value: from minus infinity to plus infinity. For nutritional values this is not the case. Nutritional values are fractions that go from 0 to an upper limit. For Energy this upper limit is 3700 kJ and for the nutrients this is 1. The Energy limit is reached if 100% of the nutrients consist of oil for instance.
That the normal distribution cannot be used is very well demonstrated by the Violin plots. Underlying the graph is the assumption of a normal distribution. This in turn leads to a plot that can go below zero.
If a normal distribution cannot be used, what should be used then? Some other probability distribution should be used.
Probability distribution
There exist many probability distributions, so which one is applicable to nutritional values. What we are looking for lies in the category of continuous distributions, which means that the nutritional values are Real numbers. And the distribution should be on a bounded interval. The most general of these distributions is the Beta distribution.
Beta distribution
The formula for the beta distribution is give in the figure below.
In the formula the values x are between 0 and 1. The α and β determine the shape of the function. No idea what kind of values these α and β will have for nutritional values.