Difference between revisions of "Country correction"
(Updated Algeria) |
(Added some words on fit function.) |
||
| Line 32: | Line 32: | ||
Instead of adding all the cities, we could fit a line to the data of a few city points. The cumulative distance of the fit at a population ratio of 1, is then again the value we are looking for. | Instead of adding all the cities, we could fit a line to the data of a few city points. The cumulative distance of the fit at a population ratio of 1, is then again the value we are looking for. | ||
| − | The function to fit must behave nicely with extrapolations. This excludes complex functions with many parameters. | + | The function to fit must behave nicely with extrapolations. This excludes complex functions with many parameters. Or functions which behave not regular outside the fitted points (polynomials). |
| + | |||
| + | This leaves the following functions: | ||
| + | * linear - results in average values; | ||
| + | * logarithmic - results in smaller values; | ||
| + | * power functions - results in larger values; | ||
In the graph for Maroc a logarithmic function is used. The largest cities are not used in the fit calculation, as these ones seem not to follow the curve. They would bias the fit to much, when we use so few points. The fit will result in a transportation size of 419 km. Compare this to a maximum actual distance of about 1000 km. | In the graph for Maroc a logarithmic function is used. The largest cities are not used in the fit calculation, as these ones seem not to follow the curve. They would bias the fit to much, when we use so few points. The fit will result in a transportation size of 419 km. Compare this to a maximum actual distance of about 1000 km. | ||
Revision as of 14:49, 6 March 2021
This page explores how the size of the country can be taken into account in the determination of the eco-score transport bonus.
Bonus approach
The eco-score approach intends to give a bonus to locally produced (and purchased) products. This bonus is +15, which is equal to a transport score of 100. This bonus is however now given to any product produced/purchased in France. No account has been taken of the very large size of France and impact of transport within the country.
Can this approach be adapted, so that the size of a country is taken into account?
Maximum bonus
It would be logic to give the maximum bonus (transport score if 100) only to very locally production and purchase. Ideally this will imply an area as small as possible, i.e. a city or very small country. Production and purchase that occurs in a country such as Andorra, Monaco, Liechtenstein or San Marino could be viewed as having a transportation score of 100.
No bonus
In the current calculation the no bonus (transportation score 0) is (arbitrarily) set at a distance of 2000 km. This distance covers roughly the size of Europe.
Centroids to the rescue
Is it possible to use the centroid calculations in determining the (transportation) size of a country?
The weighted sum for a country that consists of single city will be zero. This can then correspond to a transportation (bonus) score of 100. This means it is preferred to have no transportation.
The weighted sum of the major cities in the European Union (or larger area) could be used to define the transportation score of 0. This means a maximum transportation impact.
From Any weighted sum in between it is now possible to calculate a country transportation score. The larger the country, the lower the country transportation score. This country transportation score can be used to determine the maximum bonus for a country.
The centroid approach can also be used to calculate the country transportation size. We just have to add all cities, so that the entire population is covered. The resulting weighted distance is the size we are looking for.
In practice this approach is not feasible. It is just to much work to (to do by hand a least). So we need a way to get a reasonable approximation. For the calculation of the centroids a limited number of cities are used. We could try to extrapolate this data to get the transportation country size.
Approach
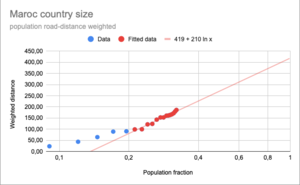
In the figure the results for Maroc are shown.
The cumulative population weighted distances are plotted against the cumulative population ratios. Each added city adds a point, increasing the cumulative population ratio and the cumulative distance. If the cumulative population ratio is 1, we have covered the entire population. And the corresponding cumulative distance is the value we are looking for.
Instead of adding all the cities, we could fit a line to the data of a few city points. The cumulative distance of the fit at a population ratio of 1, is then again the value we are looking for.
The function to fit must behave nicely with extrapolations. This excludes complex functions with many parameters. Or functions which behave not regular outside the fitted points (polynomials).
This leaves the following functions:
- linear - results in average values;
- logarithmic - results in smaller values;
- power functions - results in larger values;
In the graph for Maroc a logarithmic function is used. The largest cities are not used in the fit calculation, as these ones seem not to follow the curve. They would bias the fit to much, when we use so few points. The fit will result in a transportation size of 419 km. Compare this to a maximum actual distance of about 1000 km.
Result
This approach has been applied on the following countries:
| Country | Centroid city | size | spreadsheet |
|---|---|---|---|
| Albania | Tirana | 158 | link |
| Algeria | Algers | 777 | link |
| Austria | Vienna | 385 | link |
| Belgium | Brussels | 165 | link |
| Bosnia and Herzegovina | Zenica | 283 | link |
| Croatia | Zagreb | 236 | link |
| Czech Republic | Prague | link | |
| Denmark | Copenhagen | 271 | link |
| Estonia | Tallinn | 152 | link |
| Finland | Helsinki | link | |
| France | Paris | 1051 | link |
| Germany | Hannover | 577 | link |
| Greece | Athens | link | |
| Hungary | Budapest | link | |
| Iceland | Reykjavik | 132 | link |
| Ireland | Dublin | link | |
| Italy | Rome | 1226 | link |
| Latvia | Riga | link | |
| Lithuania | Kaunas | link | |
| Montenegro | Bijelo Polje | link | |
| Morocco | Temara | 419 | link |
| Netherlands | Utrecht | 137 | link |
| Norway | Skien | 455 | link |
| Poland | Łódź | link | |
| Portugal | Lisboa | 228 | link |
| Romania | Bucharest | 568 | link |
| Slovakia | Banská Bystrica | 254 | link |
| Slovenia | Ljubljana | 119 | link |
| Spain | Madrid | 653 | link |
| Sweden | Nörrköping | 393 | link |
| Switzerland | Olten | 158 | link |
| Tunisia | Tunis | link | |
| United Kingdom | Coventry | 347 | link |
| European Union | Munich | link | |
| Bouches du Rhône | Marseille | 25 | link |
Comments
Some observations on individual countries.
- Iceland - the weighted distance graph contains several steps, due to the addition of cities far from the centroid. This introduces strange fits, if we use all cities So only the 9 (of 20) smaller cities have been used in the fit;
Conclusion
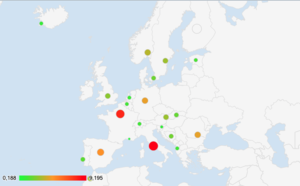
The graph below shows the malus for each country based on population road-distance weighted transportation distance. The location of the circles is on the country centroid.
Some observations:
- France and Italy have the largest malus. In order to cover the entire population a large distance is required;
- Bouches du Rhône has the smallest malus of this set;